Энергия всему голова
Обзор факторов, мешающих точной работе часов, и способов борьбы с ними начнем с рассмотрения энергетических соотношений в системе баланс-спираль. В идеальных условиях отсутствия каких-либо потерь ее колебания могут быть бесконечными (так же как у маятника), а собственная частота колебаний зависит от двух параметров — момента инерции баланса и жесткости спирали. Реальная жизнь вносит коррективы: часть энергии тратится на преодоление трения и других потерь, поэтому без внешней поддержки колебания неизбежно затухают.
Способность нашей парочки совершать колебания и противостоять внешним воздействиям определяется параметром, носящим название добротность колебательной системы. Этот термин был введен в общей теории колебаний и ее многочисленных приложениях (таких, например, как строительная механика, радиотехника, спектроскопия, а также в теории часов) в качестве «меры колебательности» динамической системы, то есть ее способности преобразовывать поступающую в нее постоянную энергию в колебательную (в случае часов постоянная энергия пружинного двигателя передается балансу через колесную систему и спуск). Добротность определяется как отношение этих энергий:
| Д = | колебательная энергия А~ |
| постоянная энергия А= |
Если считать, что поступающая энергия не меняется, то добротность системы баланс-спираль можно оценить только через ее собственные параметры. Для этого целесообразно заменить величину энергии А=на суммарную энергию потерь А0 во всех элементах колебательной системы. Тогда можно определить добротность равноценным отношением:
| Д = | колебательная энергия А~ |
| постоянная энергия А0 |
Кроме добротности, как показателя качества системы баланс-спираль в целом, в часовом деле используются и показатели качества ее отдельно взятых основных узлов: показатель качества баланса Кб, определяемый отношением
| Кб = | момент инерции баланса |
| общий вес баланса |
и показатель качества спирали Кс, определяемый отношением
| Кc = | жесткость спирали |
| общий момент трения |
Эти объективные показатели качества позволяют оценить способность системы баланс-спираль и ее узлов выполнять свои функции, обосновывать выбор основных параметров этих деталей и проводить их сравнительную оценку. Понимать, что означают и от чего зависят данные показатели важно не только разработчикам и производителям механизмов, но и покупателям и продавцам часов всех уровней, желающих всерьез разбираться в этом товаре и его качестве.
Колебательная энергия пары баланс-спираль А~ складывается из кинетической энергии движущегося баланса и потенциальной энергии свернутой спирали, определяемых, соответственно, величинами момента инерции баланса и жесткостью спирали. Отсюда понятно, что для повышения качества системы баланс-спираль необходимо максимально повысить момент инерции баланса и жесткость спирали и снизить до минимума все потери в системе. Такие же рекомендации вытекают из приведенных коэффициентов качества баланса Кб и спирали Кс.
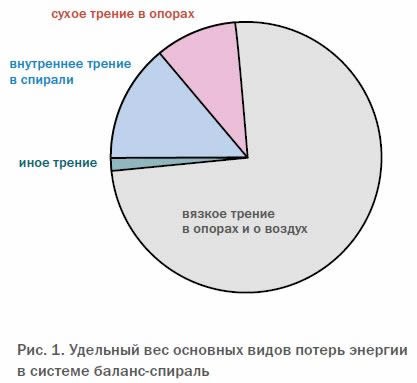
Суммарная энергия потерь в балансовых часовых колебательных системах определяется, в основном, следующими факторами:
- потерями на трение в опорах баланса (цапф о камни);
- потерями на преодоление сопротивления вращению цапф вязкой смазки опор;
- сопротивлением воздушной среды, окружающей баланс и увлекаемой им в движение;
- потерями на преодоление внутреннего (межмолекулярного) трения в материале спирали и рядом других малозначительных факторов.
На рис. 1 представлено соотношение энергий, обусловленных каждым из этих факторов. Диаграмма наглядно показывает, что самый большой вклад вносит вязкое трение, в составе которого заметно преобладают потери в опорах. По сравнению с ними остальные факторы, такие, например, как потери на трение в местах заделки концов спирали, незначительны и обычно не учитываются.
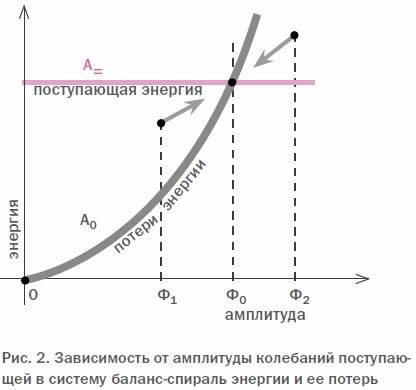
На рис. 2 показана зависимость между величиной амплитуды колебаний и энергией потерь А0. Поскольку все составляющие потерь растут или с ростом угла отклонения баланса(например, при этом увеличиваются потери на трение, преодоление вязкого сопротивления и трение в материале спирали), или с ростом его скорости (вместе со скоростью растет вязкое трение и сопротивление воздушной среды), то чем больше амплитуда, тем большими оказываются суммарные потери. Причем этот рост довольно резкий.
Этот же график наглядно иллюстрирует и сущность процесса автоматического регулирования амплитуды автоколебаний. Мы видим, что при определенной амплитуде Ф0 кривая потерь пересекает прямую А=, соответствующую поступающей в нашу колебательную систему энергии. именно с этой амплитудой будет колебаться баланс при отсутствии внешних воздействий.
Если под влиянием каких-либо внешних сил (толчков, ударов, центробежных сил и т.п.) величина амплитуды увеличится до некоторого значения Ф2, то, как видно из рис. 2, при такой амплитуде энергия потерь А0 превысит энергию привода А=, и амплитуда автоматически уменьшится сразу после прекращения действия внешней силы, стремясь вернуться к своему стационарному значению Ф0, соответствующему равенству энергии потерь и привода. При падении амплитуды до некоторого значения Ф1, меньшего Ф0, энергия привода А= превысит энергию потерь А0, вследствие чего амплитуда автоматически возрастет до своего стационарного значения Ф0.



